[Munkres Topology] 26. Compact Spaces

 This article is one of the posts in the Textbook Commentary Project.

Definition. A collection $\mathcal{A}$ of subsets of a space $X$ is said to cover $X$, or to be a covering of $X$, if the union of the elements of $\mathcal{A}$ is equal to $X$. It is called an open covering of $X$ if its elements are open subsets of $X$.

Definition. A space $X$ is said to be compact if every open covering $\mathcal{A}$ of $X$ contains a finite subcollection that also covers $X$.

Let us first porve some facts abour subspaces. If $Y$ is a subspace of $X$, a collection $\mathcal{A}$ of subsets of $X$ is said to cover $Y$ if the union of its elements contains $Y$.

Lemma 26.1. Let $Y$ be a subspace of $X$. Then $Y$ is compact if and only if every covering of $Y$ by sets open in $X$ contains a finite subcollection covering $Y$.

Proof. Suppose that $Y$ is compact and $\mathcal{A}=\{A_\alpha\}_{\alpha \in J}$ is a covering of $Y$ by sets open in $X$. Then the collection $$\{A_\alpha \cap Y | \alpha\in J\}$$ is a covering of $Y$ by sets open in $Y$; hence a finite subcollection $$\{A_{\alpha_1} \cap Y, \cdots, A_{\alpha_n} \cap Y\}$$ covers $Y$. Then $\{A_{\alpha_1},\cdots,A_{\alpha_n}\}$ is a subcollection of $\mathcal{A}$ that covers $Y$.

Conversely, suppose the given condition holds; we with to prove $Y$ compact. Let $\mathcal{A}'=\{A'_\alpha\}$ be a covering the given condition holds; we with to prove $Y$ compact. Let $\mathcal{A}'=\{A'_\alpha\}$ be a covering of $Y$ by sets open in $Y$. For each $\alpha$, choose a set $A_\alpha$ open in $X$ such that $$A'_\alpha = A_\alpha \cap Y.$$ The collection $\mathcal{A}=\{A_\alpha\}$ is a covering of $Y$ by sets open in $X$. By hypothesis, some finite subcollection $\{A_{\alpha_1},\cdots,A_{\alpha_n}\}$ covers $Y$. Then $\{A'_{\alpha_1},\cdots,A'_{\alpha_n}\}$ is a subcollection of $\mathcal{A}'$ that covers $Y$.

Theorem 26.2. Every closed subspace of a compact space is compact.

Proof. Let $Y$ be a closed subspace of the compact space $X$. Given a covering $\mathcal{A}$ of $Y$ by sets open in $X$, let us form an open covering $\mathcal{B}$ of $X$ by adjoining to $\mathcal{A}$ the single open set $X-Y$, that is, $$\mathcal{B}=\mathcal{A}\cup \{X-Y\}.$$ Some finite subcollection of $\mathcal{B}$ covers $X$. If this subcollection contains the set $X-Y$, discard $X-Y$; otherwise, leave the subcollection alone. The resulting collection is a finite subcollection of $\mathcal{A}$ that covers $Y$(drop out coverings out of $Y$, still cover $Y$.).

Theorem 26.3. Every compact subspace of a Hausdorff space is closed.

Proof. Let $Y$ be a compact subspace of the Hausdorff space $X$. We shall prove that $X-Y$ is open, so that $Y$ is closed.

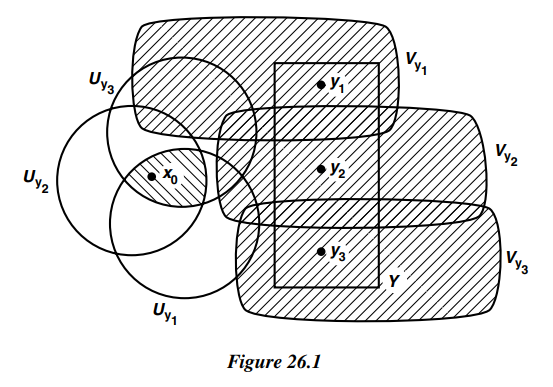
Let $x_0$ be a point of $X-Y$. We show there is a neighborhood of $x_0$ that is disjoint from $Y$. For each point $y$ of $Y$, let us choose disjoint neighborhoods $U_y$ and $V_y$ of the points $x_0$ and $y$, respectively (using the Hausdorff condtion). The collection $\{V_y |y\in Y\}$ is a covering of $Y$ by sets open in $X$; therefore, finitely many of them $V_{y_1},\cdots,V_{y_n}$ cover $Y$. The open set $$V=V_{y_1}\cup \cdots \cup V_{y_n}$$ contains $Y$, and it is disjoint from the open set $$U=U_{y_1}\cap \cdots \cap U_{y_n}$$ formed by taking the intersection of the corresponding neighborhoods of $x_0$. For if $z$ is a point of $V$, then $z\in V_{y_i}$ for some $i$, hence $z\notin U_{y_i}$ and so $z \notin U$. See Figure 26.1.

Then $U$ is a neighborhood of $x_0$ disjoint from $Y$, as desired.

Lemma 26.4. If $Y$ is a compact subspace of the Hasudorff space $X$ and $x_0$ is not in $Y$, then there exist disjoint open sets $U$ and $V$ of $X$ containing $x_0$ and $Y$, respectively.

Proof. In proof of Theorem 26.3

Theorem 26.5. The image of a compact space under a continuous map is compact.

Proof. Let $f:X\rightarrow Y$ be continuous; let $X$ be compact. Let $\mathcal{A}$ be a covering of the set $f(X)$ by sets open in $Y$. The collection $$\{f^{-1}(A)|A\in \mathcal{A}\}$$ is a collection of sets covering $X$; these sets are open in $X$ because $f$ is continuous. Hence finitely many of them, say $$f^{-1}(A_1),\cdots,f^{-1}(A_n),$$ cover $X$. Then the sets $A_1,\cdots,A_n$ cover $f(X)$.

Theorem 26.6. Let $f:X\rightarrow Y$ be a bijective continuous function. If $X$ is compact and $Y$ is Hausdorff, then $f$ is a homeomorphism.

Proof. We shall prove that images of closed sets of $X$ under $f$ are closed in $Y$; this will prove continuity of the map $f^{-1}$. If $A$ is closed in $X$, then $A$ is compact, by Theorem, 26.2. Therefore, by the theorem just proved, $f(A)$ is compact. Since $Y$ is Hausdorff, $f(A)$ is closed in $Y$, by Theorem 26.3.

Theorem 26.7. The product of finitely many compact spaces is compact.

Proof. We shall prove that the product of two compact spaces is compact; the theorem follows by induction for any finite product.

Step 1. Suppose that $x_0$ is a point of $X$, and $N$ is an open set of $X\times Y$ containing the 'slice' $x_0\times Y$ of $X\times Y$. We prove the following: $$\mbox{There is a neighborhood }W\mbox{ of }x_0\mbox{ in }X\mbox{ such that }N\mbox{ contains the entire set }W\times Y.$$ The set $W\times Y$ is often called a tube abour $x_0\times Y$.

First let us cover $x_0\times Y$ by basis elements $U\times V$ (for the topology of $X\times Y$) lying in $N$. The space $x_0\times Y$ is compact, being homeomorphic to $Y$. Therefore, we can cover $x_0\times Y$ by finitely many such basis elements $$U_1\times V_1,\cdots,U_n\times V_n.$$ (We assume that each of the basis elements $U_i\times V_i$ actually intersects $x_0\times Y$, since otherwise that basis element would be superfluous; we could discard it from the finite collection and still have a covering of $x_0\times Y$.) Define $$W=U_1\cap \cdots\cap U_n.$$ The set $W$ is open, and it contains $x_0$ because each set $U_i\times V_i$ intersects $x_0\times Y$.

We assert that the sets $U_i\times V_i$, which were chosen to cover the slice $x_0\times Y$, actually cover the tube $W\times Y$. Let $x\times y$ be a point of $W\times Y$. Consider the point $x_0\times y$ of the slice $x_0\times Y$ having the same $y$-coordinate as this point. Now $x_0\times y$ belongs to $U_i\times V_i$ for some $i$, so that $y\in V_i$. Bur $x\in U_j$ for every $j$ (because $x\in W$). Therefore, we have $x\times y\in U_i\times V_i$, as desired. (Get finite choose of cover $W$)

Since all the sets $U_i\times V_i$ lie in $N$, and since they cover $W\times Y$, the tube $W\times Y$ lies in $N$ also. See Figure 26.2.

Step 2. Now we prove the theorem. Let $X$ and $Y$ be compact spaces. Let $\mathcal{A}$ ($\{U_i\timesV_i\}$) be an open covering of $X\times Y$. Given $x_0\in X$, the slice $x_0\times Y$ is compact and be an open covering of $X\times Y$. Given $x_0\times X$, the slice $x_0\times Y$ is compact and may therefore be covered by finitely many elements $A_1,\cdots,A_m$ of $\mathcal{A}$. Their union $N=A_1\cup \cdots \cup A_m$ is an open set containing $x_0\times Y$; by Step 1, the open set $N$ contains a tube $W\times Y$ abour $x_0\times Y$, where $W$ is open in $X$. Then $W\times Y$ is covered by finitely many elements $A_1,\cdots,A_m$ of $\mathcal{A}$.

Thus, for each $x$ in $X$, we can choose a neighborhood $W_x$ if $x$ such that the tube $W_x\times Y$ can be covered by finitely many elements of $\mathcal{A}$. The collection of all the neighborhoods $W_x$ is an open covering of $X$; therefore by compactness of $X$, there exists a fintie subcollection $$\{W_1,\cdots,W_k\}$$ covering $X$. The union of the tubes $$W_1\times Y,\cdots,W_k\times Y$$ is all of $X\times Y$; since each may be covered by finitely many elements of $\mathcal{A}$, so may $X\times Y$ be covered.

Lemma 26.8 (The tube lemma). Consider the product space $X\times Y$, where $Y$ is compact. If $N$ is an open set of $X\times Y$ containing the slice $x_0\times Y$ of $X\times Y$, then $N$ contains some tube $W\times Y$ abour $x_0\times Y$, where $W$ is a neighborhood of $x_0$ in $X$.

Proof. Step 1 of Theorem 26.7

Definition. A collection (can be infinite) $\mathcal{C}$ of subsets of $X$ is said to have the finite intersection property if for every finite subcollection $$\{C_1,\cdots,C_n\}$$ of $\mathcal{C}$, the intersection $C_1\cap \cdots\cap C_n$ is nonempty.

Theorem 26.9. Let $X$ be a topological space. Then $X$ is compact if and only if for every (infinite) collection $\mathcal{C}$ of closed sets in $X$ having the finite intersection property, the intersection $\bigcap_{C\in\mathcal{C}} C$ of all the (infinite) elements of $\mathcal{C}$ is nonempty.

Proof. Given a collection $\mathcal{A}$ of subsets of $X$, let $$\mathcal{C}=\{X-A|A\in \mathcal{A}\}$$ be the collection of their complements. Then the following statements hold:

(1) $\mathcal{A}$ is a collection of open sets if and only if $\mathcal{C}$ is a collection of closed sets.

(2) The collection $\mathcal{A}$ covers $X$ is and only if the intersection $\bigcap_{C\in \mathcal{C}}C$ of all the elements of $\mathcal{C}$ is empty.

(3) The finite subcollection $\{A_1,\cdots,A_n\}$ of $\mathcal{A}$ covers $X$ is and only if the intersection of the corresponding (finite) element $C_i=X-A_i$ of $\mathcal{C}$ is empty.

The first statement is trivial, while the second and third follow from DeMorgan's law: $$X-(\bigcup_{\alpha\in J} A_\alpha)=\bigcap_{\alpha\in J}(X-A_\alpha).$$

The proof of the theroem now proceeds in two easy steps: taking the contrapositive (of the theorem), and then the complement (of the sets).

The statement that $X$ is compact is equivalent to saying: 'Given any collection $\mathcal{A}$ of open subsets of $X$, if $\mathcal{A}$ covers $X$, then some finite subcollection of $\mathcal{A}$ covers $X$.' This statement is equivalent to its contrapositive, which is the following: 'Given any collection $\mathcal{A}$ of open sets, if no finite subcollection of $\mathcal{A}$ covers $X$, then $\mathcal{A}$ does not cover $X$.' Letting $\mathcal{C}$ be, as earlier, the collection $\{X-A|A\in \mathcal{A}\}$ and applying (1)-(3), we see that this statement is in turn equivalent to the following: 'Given any collection $\mathcal{C}$ of closed sets, if every finite intersection of elements of $\mathcal{C}$ is nonempty, then the intersection of all the elements of $\mathcal{C}$ is nonempty.' This is just the condition of our theorem. wow.. PERFECT PROOF!

A special case of this theorem occurs when we have a nested sequence $C_1\supset C_2 \supset \cdots \supset C_n \supset C_{n+1} \supset \cdots$ of closed sets in a compact space $X$. If each of the sets $C_n$ is nonempty, then the collection $\mathcal{C}=\{C_n\}_{n\in \mathbb{Z}_+}$ automatically has the finite intersection property. Then the intersection $$\bigcap_{n\in \mathbb{Z}_+} C_n$$ is nonempty.