[Munkres Topology] 28. Limit Point Compactness

 This article is one of the posts in the Textbook Commentary Project.

Definition. A space $X$ is said to be limit point compact if every infinite subset of $X$ has a limit point.

Theorem 28.1. Compactnmess implies limit point compactness, but not conversely.

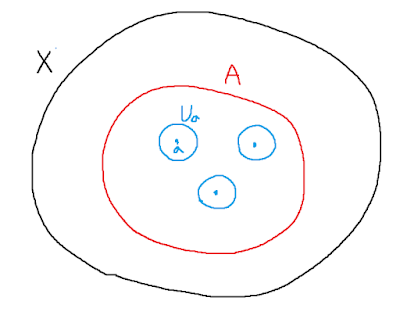
Proof. Let $X$ be a compact space. Given a subset $A$ of $X$, we wish to prove that if $A$ is infinite, then $A$ has a limit point. We prove the contrapositive- if $A$ has no limit point, then $A$ must be finite.

So suppose $A$ has no limit point. Then $A$ contains all its limit points(nothing), so that $A$ is closed. Furthermore, for each $a\in A$ we can choose a neighborhood $U_a$ of $a$ such that $U_a$ intersects $A$ in the point $a$ alone. The space $X$ is covered by the open set $X-A$ and the open sets $U_a$; being compact, it can be covered by finitely many of these sets. Since $X-A$ does not intersect $A$, and each set $U_a$ contains only one point of $A$, the set $A$ must be finite.

Definition. Let $X$ be a topological space. If $(x_n)$ is a sequence of points of $X$, and if $$n_1<n_2<\cdots <n_i<\cdots$$ is an increasing sequence of positive integers, then the sequence $(y_i)$ defined by setting $y_i=x_{n_i}$ is called a subsequence of the sequence $(x_n)$. The space $X$ is said to be sequentially compact if every sequence of points of $X$ has a convergent subsequence.

Theorem 28.2. Let $X$ be a metrizable space, Then the following are equivalent:

(1) $X$ is compact.

(2) $X$ is limit point compact.

(3) $X$ is sequentially compact.

Proof.

We have already proved that (1)$\Rightarrow$(2). To show that (2)$\Rightarrow$(3), assume that $X$ is limit point compact. Given a sequence $(x_n)$ of points of $X$, consider the set $A=\{ x_n | n \in \mathbb{Z}_+\}$. If the set $A$ is finite, then there is a point $x$ such that $x=x_n$ for infinitely many values of $n$. In this case, the sequence $(x_n)$ has a subsequence that is constant, and therefore converges trivially. On the other hand, if $A$ is infinite, then $A$ has a limit point $x$. We define a subsequence of $(x_n)$ converging to $x$ as follows: First choose $n_1$ so that $$x_{n_1}\in B(x,1).$$ Then suppose that the positive integer $n_{i-1}$ is given. Because the ball $B(x,1/i)$ intersects $A$ in infinitely many points, we can choose an index $n_i > n_{i-1}$ such that $$x_{n_i} \in B(x,1/i).$$ Then the subsequence $x_{n_1},x_{n_2},\cdots$ converges to $x$. (Since infinite, we can choose always different point)

Finally, we show that (3)$\Rightarrow$(1). This is the hardest part of the proof...

First, we show that if $X$ is sequentially compact, then the Lebesgue number lemma holds for $X$. (This would follow from compactness, but compactness is what we are trying to prove!: Lebesgue number lemma is not enough.) Let $\mathcal{A}$ be an open covering of $X$. We assume that there is no $\delta>0$ such that each set of diameter less than $\delta$ has an element of $\mathcal{A}$ containing it, and derive a contradiction.

Our assumption implies in particular that for each positive integer $n$, there exists a set of diameter less than $1/n$ that is not contained in any element of $\mathcal{A}$; let $C_n$ be such a set. Choose a point $x_n \in C_n$, for each $n$. By hypothesis, some subsequence $(x_{n_i})$ of the sequence $(x_n)$ converges, say to the point $a$. Now $a$ belongs to some element $A$ of the collection $\mathcal{A}$; because $A$ is open, we may choose an $\epsilon>0$ such that $B(a,\epsilon)\subset A$. If $i$ is large enough that $1/n_i < \epsilon/2$, then the set $C_{n_i}$ lies in the $\epsilon/2$-neighborhood of $x_{n_i}$; if also chosen large enough that $d(x_{n_i},a)<\epsilon/2$, then $C_{n_i}$ lies in the $epsilon$-neighborhood of $a$. But this means that $C_{n_i}\subset A$, contrary to hypothesis.

Second, we show that if $X$ is sequentially compact, then given $\epsilon>0$, there exists a finite covering of $X$ by open $\epsilon$-balls. Once again, we proceed by contradiction. Assume that there exists an $\epsilon>0$ such that $X$ cannot be covered by finitely many $\epsilon$-balls. Construct a sequence of points $x_n$ of $X$ as follows: First, choose $x_1$ to be any point of $X$. Noting that the ball $B(x_1,\epsilon)$ is not all of $X$ (otherwise $X$ could be covered by a single-$\epsilon$-ball), choose $x_2$ to be a point of $X$ not in $B(x_1,\epsilon)$. In general, given $x_1,\cdots,x_n$, choose $x_{n+1}$ to be a point not in the union $$B(x_1,\epsilon)\cup \cdots \cup B(x_n,\epsilon),$$ using the fact that these balls do not cover $X$. Note that by construction $d(x_{n+1},x_i)\ge \epsilon$ for $i=1,\cdots,n$. Theresore, the sequence $(x_n)$ can have no convergent subsequence; in fact, any ball of radius $\epsilon/2$ can contain $x_n$ for at most one value of $n$.

Finally, we show that if $X$ is sequentially compact, then $X$ is compact. Let $\mathcal{A}$ be an open covering of $X$. Because $X$ is sequentially compact, the open covering $\mathcal{A}$ has a Lebesgue number $\delta$. Let $\epsilon=\delta/3$; use sequential compactness of $X$ to find a finite covering of $X$ by open $\epsilon$-balls. Each of these balls has diameter at most $2\delta/3$, so it lies in an element of $\mathcal{A}$. Choosing one such element of $\mathcal{A}$ for each of these $\epsilon$-balls, we obtain a finite subcollaction of $\mathcal{A}$ that covers $X$.