[Munkres Topology] 31. The Separation Axioms

 This article is one of the posts in the Textbook Commentary Project.

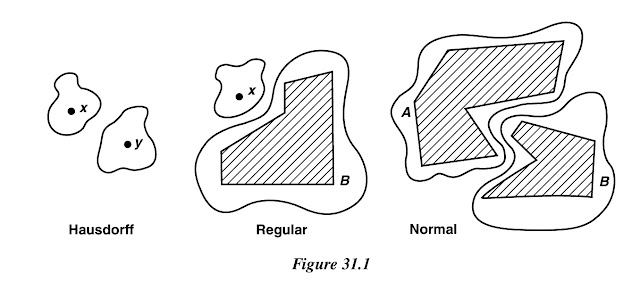
Definition. Suppose that one-point sets are closed in $X$. Then $X$ is said to be regular if for each pair consisting of a point $x$ and a closed set $B$ disjoint from $x$, there exists disjoint open sets containing $x$ and $B$, respectively. The space $X$ is said to be normal if for each pair $A$, $B$ of disjoint closed sets of $X$, there exists disjoint open sets containing $A$ and $B$, respectively.

Lemma 31.1. Let $X$ be a topological space. Let one-point sets in $X$ be closed.

(a) $X$ is regular if and only if given a pint $x$ of $X$ and a neighborhood $U$ of $x$, there is a neighborhood $V$ of $x$ such that $\bar{V}\subset U$.

(b) $X$ is normal if and only if given a closed set $A$ and an open set $U$ containing $A$, there is an open set $V$ containing $A$ such that $\bar{V}\subset U$.

Proof. 

(a) Suppose that $X$ is regular. and suppose that the point $x$ and the neighborhood $U$ of $x$ are given. Let $B=X-U$; then $B$ is a closed set. By hypothesis, there exist disjoint open sets $V$ and $W$ containing $x$ and $B$, respectively. The set $\bar{V}$ is disjoint from $B$, since if $y\in B$, the set $W$ is a neighborhood of $y$ disjoint from $V$. Therefore, $\bar{V}\subset U$, as desired. 

To prove the converse, suppose the point $x$ and the closed set $B$ not containing $x$ are given Let $U=X-B$. By hypothesis, there is a neighborhood $V$ of $x$ such that $\bar{V}\subset U$. The open sets $V$ and $X-\bar{V}$ are disjoint open sets containing $x$ and $B$, respectively. Thus $X$ is regular.

(b) Same as (a), replaces the point $x$ by the set $A$.

Theorem 31.2. (a) A subspace of a Hausdorff space is Hausdorff; a product of Hausdorff spaces is Hausdorff.

(b) A subspace of a regular space if regular; a product of regular spaces is regular.

Proof. 

(a) Let $X$ be Hausdorff. Let $x$ and $y$ be two points of the subspace $Y$ of $X$. If $U$ and $V$ are disjoint neighborhoods in $X$ of $x$ and $y$, respectively, then $U\cap Y$ and $V\cap Y$ are disjoint neighborhoods in $X$ of $x$ and $y$, respectively, then $U\cap Y$ and $V\cap Y$ are disjoint neighborhoods of $x$ and $y$ in $Y$.

Let $\{X_\alpha \}$ be a family of Hausdorff spaces. Let $\mathbf{x}=(x_\alpha)$ and $\mathbf{x}=(y_\alpha)$ be distinct points of the product space $\prod X_\alpha$. Because $\mathbf{x}\ne \mathbf{y}$, there is some index $\beta$ such that $x_\beta \ne y_\beta$. Choose disjoint open sets $U$ and $V$ in $X_\beta$ containing $x_\beta$ and $y_\beta$, respectively. Then the sets $\pi_\beta^{-1} (U)$ and $\pi_\beta^{-1}(V)$ are disjoint open sets in $\prod X_\alpha$ containing $\mathbf{x}$ and $\mathbf{y}$, resepctively.

(b) Let $Y$ be a subspace of the regular space $X$. Then one-point sets are closed in $Y$. Let $x$ be a point of $Y$ and let $B$ be a closed subset of $Y$ disjoint from $x$. Now $\bar{B}\cap Y=B$, where $\bar{B}$ denotes the closure of $B$ in $X$. Therefore, $x\notin \bar{B}$, so, using regularity of $X$, we can choose disjoint open sets $U$ and $V$ of $X$ containing $x$ and $\bar{B}$, respectively. Then $U\cap Y$ and $V\cap Y$ are disjoint open sets in $Y$ containing $x$ and $B$, respectively.

Let $\{X_\alpha\}$ be a family of regular spaces; let $X=\prod X_\alpha$. By (a), $X$ is Hausdorff, so that one-point sets are closed in $X$. We use the preceding lemma to prove regularity that one-point sets are closed in $X$. We use the preceding lemma to prove regularity of $X$. Let $\mathbf{x}=(x_\alpha)$ be a point of $X$ and let $U$ be a neighborhood of $\mathbf{x}$ in $X$. Choose a basis element $\prod U_\alpha$ abour $\mathbf{x}$ obtained in $U$. Choose, for each $\alpha$, a neighborhood $V_\alpha$ of $x_\alpha$ in $X_\alpha$ such that $\bar{V}_\alpha \subset U_\alpha$; if it happens that $U_\alpha = X_\alpha$, choose $V_\alpha =X_\alpha$. Then $V=\prod V_\alpha$ is a neighborhood of $x$ in $X$. Since $\bar{V}=\prod \bar{V}_\alpha$ by Theorem 19.5, it follows at once that $\bar{V}\subset \prod U_\alpha \subset U$, so that $X$ is regular (Lemma 31.1).