[Munkres Topology] 34. The Урысо́н Metrization Theorem

 This article is one of the posts in the Textbook Commentary Project.

Theorem 34.1 (Urysohn metrization theorem). Every regular space $X$ with a countable basis is metrizable($\mathbb{R}^\omega$).

Proof. We shall prove that $X$ is metrizable by imbedding $X$ in a metrizable space $Y$; that is, by showing $X$ homeomorphic with a subspace of $Y$. The two versions of the proof differ in the choice of the metrizable space $Y$. In the first version, $Y$ is the space $\mathbb{R}^\omega$ in the product topology, a space that we have previously proved to be metrizable (Theorem 20.5). In the second version, the space $Y$ is also $\mathbb{R}^\omega$, but this time in the topology given by the uniform metric $\bar{\rho}$. In each case, it turns out that our construction actually imbeds $X$ in the subspace $[0,1]^\omega$ of $\mathbb{R}^\omega$.

Step 1. We proved the following: There exists a countable collection of continuous functions $f_n:X\rightarrow [0,1]$ having the property that given any point $x_0$ of $X$ and any neighborhood $U$ of $x_0$, there exists an index $n$ such that $f_n$ is positive at $x_0$ and vanishes outside $U$. (See Figure 34.2)

It is a consequence of the Urysohn lemma that, given $x_0$ and $U$, there exists such a function. However, if we choose one such function for each pair $(x_0,U)$, the resulting collection will not in general be countable. Our task is to cut the collection down to size. Here is one way to proceed:

Let $\{B_n\}$ be a countable basis for $X$. For each pair $n$, $m$ of indices for which $\bar{B}_n\subset B_m$, apply the Urysohn lemma to choose a continuous function $g_{n,m}:X\rightarrow [0,1]$ such that $g_{n,m}(\bar{B}_n)=\{1\}$ and $g_{n,m}(X-B_m)=\{0\}$. Then the collection $\{g_{n,m}\}$ satisfies our requirement: Given $x_0$ and given a neighborhood $U$ of $x_0$, one can choose a basis element $B_m$ containing $x_0$ that is contained in $U$. (See fIgure 34.3)Using regularity, one can then choose $B_n$ so that $x_0\in B_n$ and $\bar{B}_n\subset B_m$. Then $n$, $m$ is a pair of indices for which the function $g_{n,m}$ is defined; and it is positive at $x_0$ and vanishes outside $U$. Because the collection $\{g_{n,m}\}$ is indexed with a subset of $\mathbb{Z}_+\times \mathbb{Z}_+$, it is countable; therefore it can be reindexed with the positive integers, giving us the desired collection $\{f_n\}$.

Step 2 (First version of the proof). Given the functions $f_n$ of Step 1, take $\mathbb{R}^\omega$ in the product topology and defined a map $F:X\rightarrow \mathbb{R}^\omega$ by the rule $$F(x)=(f_1(x),f_2(x),\cdots).$$ We assert that $F$ is an imbedding.

First, $F$ is continuous because $\mathbb{R}^\omega$ has the product topology and each $f_n$ is continuous. Second, $F$ is injective because given $x\ne y$, we know there is an index $n$ such that $f_n(x)>0$ and $f_n(y)=0$; (since for any $U$.) therefore, $F(x)\ne F(y)$.

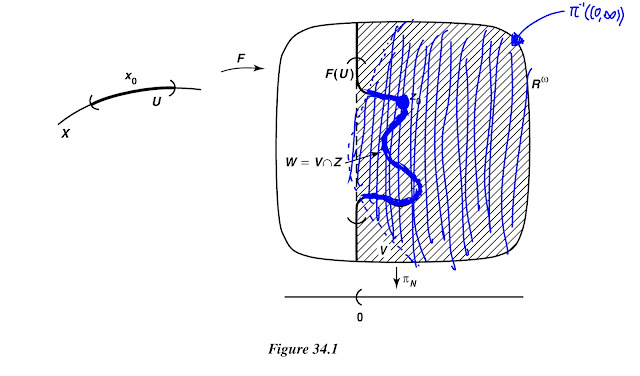
Finally, we must prove that $F$ is a homeomorphism of $X$ onto its image, the subspace $Z=F(X)$ of $\mathbb{R}^\omega$. We know that $F$ defines a continuous bijection of $X$ with $Z$, so we need only show that for each open set $U$ in $X$, the set $F(U)$ is open in $Z$. Let $z_0$ be a point of $F(U)$. We shall find an open set $W$ of $Z$ such that $$z_0\in W \subset F(U).$$

Let $x_0$ be the point of $U$ such that $F(x_0)=z_0$. Choose an index $N$ for which $f_N(x_0)>0$ and $f_N(X-U)=\{0\}$. Take the open ray $(0,+\infty)$ in $\mathbb{R}$, and let $V$ be the open set $$V=\pi_N^{-1}((0,+\infty))$$ of $\mathbb{R}^\omega$, Let $W=V\cap Z$; then $W$ is open in $Z$, by definition of the subspace topology. See Figure 34.1. We assert that $z_0\in W\subset F(U)$. First, $z_0\in W$ because $$\pi_N(z_0)=\pi_N(F(x_0))=f_N(x_0)>0.$$( $f_N$ appear from definition of $F$.) Second, $W\subset F(U)$. For if $z\in W$, then $z=F(x)$ for some $x\in X$, and $\pi_N(z)\in (0,+\infty)$. Since $\pi_N(z)=\pi_N(F(x))=f_N(x)>0$, and $f_N$ vanishes outside $U$, the point $x$ must be in $U$. Then $z=F(x)$ is in $F(U)$, as desired.

Thus $F$ is an imbedding of $X$ in $\mathbb{R}^\omega$.

Step 3 (Second version of the proof). In this version, we imbed $X$ in the metric space $(\mathbb{R}^\omega,\bar{\rho})$. Actually, we imbed $X$ in the subspace $[0,1]^\omega$, on which $\bar{\rho}$ equals the metric $$\rho(\mathbf{x},\mathbf{y})=\sup \{ |x_i - y_i|\}.$$ We use the countable collection of functions $f_n:X\rightarrow [0,1]$ constructed in Step 1. But now we impose the addition that $f_n(x)\le 1/n$ for all $x$. (This condition is easy to satisfy; we can just divide each function $f_n$ by $n$.)

Define $F:X\rightarrow [0,1]^\omega$ by the equation $$F(x)=(f_1(x),f_2(x),\cdots)$$ as before. We assert that $F$ is now an imbedding relative to the metric $\rho$ on $[0,1]^\omega$. We know from Step 2 that $F$ is injective. Furthermore, we know that if we use the product topology on $[0,1]^\omega$, the map $F$ carries open sets of $X$ onto open sets of the subspace $Z=F(X)$. This statement remains true if one passes to the finer (larger) topology on $[0,1]^\omega$ induced by the metric $\rho$.

The one thing left to do is to prove that $F$ is continuous. This does not follow from the fact that each component function is continuous, for we are not using the product topology on $\mathbb{R}^\omega$ now. Here is where the assumption $f_n(x)\le 1/n$ comes in.

Let $x_0$ be a point of $U$, and let $\epsilon >0$. To prove continuity, we need to find a neighborhood $U$ of $x_0$ such that $$x\in U\Rightarrow \rho(F(x),F(x_0))<\epsilon .$$ First choose $N$ large enough that $1/N\le \epsilon/2$. Then for each $n=1,\cdots,N$ use the continuity of $f_n$ to choose a neighborhood $U_n$ of $x_0$ such that $$\left| f_n(x)-f_n(x_0)\right| \le \epsilon/2$$ for $x\in U_n$. Let $U=U_1\cap \cdots\cap U_N$; we show that $U$ is the desired neighborhood of $x_0$. Let $x\in U$. If $n\le N$, $$\left| f_n(x)-f_n(x_0)\right| \le \epsilon/2$$ by choice of $U$. And if $n>N$, then $$\left| f_n(x)-f_n(x_0)\right| < 1/N\le \epsilon/2$$ because $f_n$ maps $X$ into $[0,1/n]$. Therefore for all $x\in U$, $$\rho (F(x),F(x_0))\le \epsilon/2 < \epsilon,$$ as desired.

Theorem 34.2 (Imbedding theorem). Let $X$ be a space in which one-point sets are closed. Suppose that $\{f_\alpha\}_{\alpha \in J}$ is an indexed faimily of continuous functions $f_\alpha :X\rightarrow \mathbb{R}$ satisfying the requirement that for each point $x_0$ of $X$ and each neighborhood $U$ of $x_0$, there is an index $\alpha$ such that $f_\alpha$ is positive at $x_0$ and vanishes outside $U$. Then the function $F:X\rightarrow \mathbb{R}^J$ defined by $$F(x)=(f_\alpha (x))_{\alpha\in J}$$ is an imbedding of $X$ in $\mathbb{R}^J$. If $f_\alpha$ maps $X$ into $[0,1]$ for each $\alpha$, then $F$ imbeds $X$ in $[0,1]^J$.

Proof. Same as step 2, $n\rightarrow \alpha$, $\mathbb{R}^\omega\rightarrow \mathbb{R}^J$.

Theorem 34.3. A space $X$ is completely regular if and only if it is homeomorphic to a subspace of $[0,1]^J$ for some $J$.