[Nakahara GTP] 12.8 The Atiyah–Patodi–Singer index theorem
This article is one of Manifold, Differential Geometry, Fibre Bundle.
12.8.1 $\eta$-invariant and spectral flow
Let $i\nabla\!\!\!\! /$ be a Hermitian Dirac operator defined on an odd-dimensional manifold $M$, $\dim M=2l+1$. Since $i\nabla\!\!\!\! /$ is Hermitian, the eigenvalues $\lambda_k$ are real. We define the $\eta$-invariant of $i\nabla\!\!\!\! /$ by the spectral asymmetry of $i\nabla\!\!\!\! /$, $$\begin{align}\eta\equiv \sum_{\lambda_k>0}1-\sum_{\lambda_k<0}1.\end{align}$$ This is not well defined and requires a proper regularizationi. For example, we may defined $\eta$ by $\lim_{s\rightarrow 0}\eta(s)$ where $$\begin{align}\eta(s)\equiv \sum_k'\mbox{sgn}(\lambda_k)|\lambda_k|^{-2s}\quad \mbox{Re} s>0.\end{align}$$ It can be shown that, under proper boundary conditions, $\eta(s)$ has no pole at $s=0$.
Exercise 12.7. User the Mellin transformation $$\frac{1}{2}\Gamma\left( \frac{s+1}{2}\right)a^{-(s+1)/2}=\int^\infty_0 dx\, x^se^{-ax^2}\quad a>0$$ to verify that $$\begin{align}\eta(s)=\frac{2}{\Gamma(\frac{1}{2}(s+1))}\int^\infty_0dx\, x^s\mbox{tr} i\nabla\!\!\!\! / e^{-x^2(i\nabla \!\!\! /)^2}.\end{align}$$
Suppose a Dirac field is interacting with an external gauge potential $\mathcal{A}_t$, $t\in[0,1]$. The Dirac operator $i\nabla\!\!\!\! /(\mathcal{A}_t)$ has a $t$-dependent eigenvalue problem. If an eigenvalue of $i\nabla\!\!\!\! /(\mathcal{A}_t)$ crosses zero, the $\eta$-invariant jumps by $\pm 2$. This jump denotes the spectral flow from $\lambda \gtrless 0$ modes to $\lambda \lessgtr 0$ modes; if $\eta$ jumps by $+2$ ($-2$), there is a flow of a state from $\lambda<0$ to $\lambda>0$ ($\lambda>0$ to $\lambda<0$), see figure 12.1. In addition to the discontinuous change associated with the spectral flow, $i\nabla\!\!\!\! /$ also has a continuous variation $\eta_c$. We have $$\begin{align}\eta(t=1)-\eta(t=0)=\int^1_0dt\frac{d\eta_c}{dt}+2\times (\mbox{spectral flow}).\end{align}$$
12.8.2 The Atiyah–Patodi–Singer (APS) index theorem
Let us consider a $(2l+2)$-dimensional Dirac operator $$\begin{align} i\hat{D}_{2l+2}=i\sigma_1\frac{\partial}{\partial t}+\sigma_2\otimes i\nabla\!\!\!\! /(\mathcal{A}_t)=\begin{pmatrix}0&D\\ D^\dagger&0\end{pmatrix}\end{align}$$ where $$\begin{align}D=i\partial_t-\nabla\!\!\!\! /(\mathcal{A}_t)\quad D^\dagger=i\partial_t+\nabla\!\!\!\! /(\mathcal{A}_t).\end{align}$$ (Remark: The position of $D$ and $D^\dagger$ are reversed since $$\gamma^{2l+3}=\begin{pmatrix}-\mathbf{1}&0\\0&\mathbf{1}\end{pmatrix}$$ for our choice of $\gamma$-matrice)
Theorem 12.3. (Atiyah-Patodi-Singer theorem) Let $M$ be an odd-dimensional manifold and $i\nabla\!\!\!\! /(\mathcal{A}_t)$ a Dirac operator on $M$ interacting with an external gague field $\mathcal{A}_t$. Then ,$$\begin{align}\mbox{ind}D=\dim\ker D-\dim\ker D^\dagger \nonumber\\ =\int_{M\times I}\hat{A}(\mathcal{R})\mbox{ch}(\mathcal{F})|_{vol}-\frac{1}{2}[\eta(i\nabla\!\!\!\! /(\mathcal{A}_1))-\eta(i\nabla\!\!\!\! /(\mathcal{A}_0))].\end{align}$$
The general argument shows that the continuous part $\eta_c$ of the $\eta$-invariant satisfies $$\begin{align}\int^1_0dt\frac{d\eta_c}{dt}=2\int_{M\times I}\hat{A}(\mathcal{R})\mbox{ch}(\mathcal{F})|_{vol}.\end{align}$$
The RHS of (7) is simply the spectral flow $$-\frac{1}{2}[\eta(t=1)-\eta(t=0)]+\frac{1}{2}\int_0^1dt\frac{\eta_c}{dt}=-\mbox{spectral flow}.$$ Thus, we find another expression for the APS index theorem, $$\begin{align}\mbox{ind} i\hat{D}_{2l+2}=-\mbox{spectral flow}.\end{align}$$ We use the APS index theorem to study the odd-dimensional parity anomaly in section 13.6.
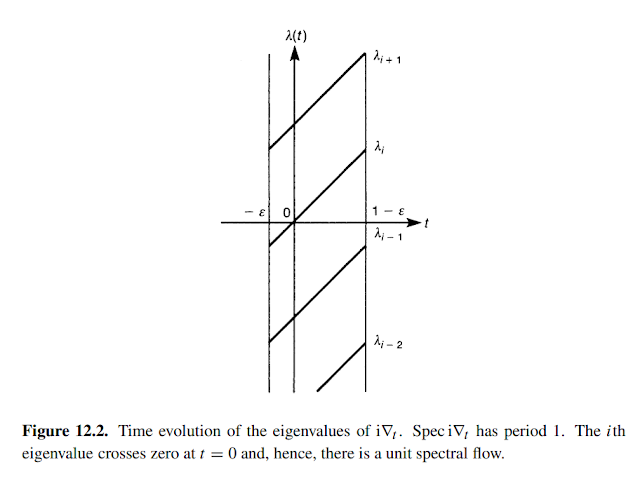
Example 12.8. Let $M=S^1$ and $\theta$ be its coordinate. Consider a Hermitian operator $$\begin{align}i\nabla_t\equiv i\left(\frac{\partial}{\partial \theta}-it\right) = i\partial_\theta+t\quad i\in \mathbb{R}.\end{align}$$ The term $-it$ is thought of as a $U(1)$ gauge potential. The eigenvector and the eigenvalue of $i\nabla_t$ are $$\psi_{n,t}(\theta)=\frac{1}{\sqrt{2\pi}}e^{-in\theta}\ (n\in \mathbb{Z})\quad \lambda_n(t)=n+t.$$ Since $\mbox{Spec}i\nabla_t=\mbox{Spec}i\nabla_{t+1}$, the family of operators $i\nabla_t$ is periodic in $t$ with the period $1$, see figure 12.2. This periodicity manifests itself in the gauge equivalence of $i\nabla_t$ and $i\nabla_{t+1}$: $$i\nabla_{t+1}=e^{i\theta}i\nabla_te^{-i\theta}.$$ There is precisely unit spectral flow from $\lambda<0$ to $\lambda>0$ at $t=0$ while $t$ changes from $-\epsilon$ to $1-\epsilon$, $\epsilon$ being a small positive number. From $i\nabla_t$, we construct a two-dimensional Dirac operator $$\begin{align}iD\!\!\!\! /_2\equiv i\sigma_2\otimes \frac{\partial}{\partial t}+\sigma_2\otimes i\nabla_t=\begin{pmatrix}0&D\\ D^\dagger&0\end{pmatrix}\end{align}$$ where $$\begin{align}D\equiv i\partial_t+\partial_\theta-it\quad D^\dagger\equiv i\partial_t-\partial_\theta+it.\end{align}$$ These operators act on functions which satisfy the boundary conditions $$\begin{align}\phi(\theta+2\pi,t)=\phi(\theta,t)\quad \phi(\theta,t+1)=e^{i\theta}\phi(\theta,t).\end{align}$$
Let $\phi_0\in \ker D^\dagger$. We have a Fourier expansion $$\phi_0(\theta,t)=\sum a_n(t)e^{-in\theta}.$$ It follows from $D^\dagger\phi_0=0$ that $$a_n'(t)+(n+t)a_n(t)=0$$ which is easily solved to yield $$a_n(t)=c_n\exp \left( -\frac{(n+t)^2}{2}\right).$$ The boundary conditions (13) require that $$\sum_nc_n\exp \left( -\frac{(n+t+1)^2}{2}\right) e^{-in\theta}=\sum_nc_n\exp\left( -\frac{(n+t)^2}{2}\right) e^{-i(n-1)\theta}$$ from which we find that $c_n$ is independent of $n$. Thus, $\ker D^\dagger$ is one dimensional and is spanned by the theta function, $$\begin{align}\phi_0(\theta,t)=\sum \exp \left( -\frac{(n+t)^2}{2}-in\theta\right).\end{align}$$ Suppose $\tilde{\phi}_0(\theta,t)\in\ker D$. If we put $\tilde{\phi}_0(\theta,t)=\sum b_n(t)e^{-in\theta}$, $b_n(t)$ satisfies $$b'_n(t)-(n+t)b_n(t)=0.$$ The solution of this equation is $$b_n(t)=b_n(0)\exp\frac{(n+t)^2}{2}$$ and, hence $\tilde{\phi}_0$ cannot be normalized. This shows that $$\mbox{ind} D=\dim\ker D-\dim\ker D^\dagger=-1$$ which agrees with $-\mbox{(spectral flow)}$.